Вокруг нас есть много примеров волновых процессов.
Стандартный метод, с помощью которого
физика доказывает, что в данной системе в самом деле должны существовать
волны, это получение некоего дифференциального уравнения
второго порядка в частных производных, известного под именем волнового уравнения:
д2f(x,t)/дt2 √ v2 д2f(x,t)/дx2 = 0.
Здесь д это значок частной производной, а v ≈ это скорость волны.
После того, как это уравнение выведено, все рады и говорят, что в нашей
системе есть волновое движение.
Где-то в районе первого курса университета это уравнение
меня смущало. Ну да, если подставить туда синус, получится все правильно,
и даже если подставить любую функцию, зависящую только от разности
x√vt, то и она оказывалась решением этого уравнения.
Однако как почувствовать, что это уравнение с неизбежностью
есть именно то уравнение, которое описывает волны? Можно ли вывести его,
не привязываясь к какой-то конкретной волне в какой-то конкретной системе,
а просто чтоб из одних только слов "бегущая волна" получить это уравнение?
Некоторое время спустя я придумал некий вывод, которых хочу показать вам.
Я не претендую на нечто новое, я просто предлагаю взглянуть на известные
уже вещи с другой точки зрения.
Итак, я стартую со слов "бегущая волна". Что это значит?
Это значит, что тот объект, для которого мы хотим найти уравнение,
есть нечто, смещающееся в пространстве. Разумеется, это не просто
движение какого-то тела, а смещающийся профиль какого-то распределения,
неважно какого.
| ═ |
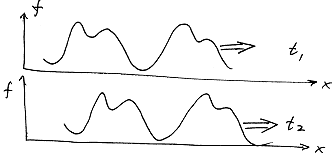
Рис.1 Бегущая волна.
═
|
Волны бывают разные, но давайте сейчас получим уравнение,
описывающее волну, которая бежит вперед без изменения своей формы.
Профиль f(x,t), нарисованный на Рис.1, как раз подходит под наше определение
бегущей и неизменяющейся волны.
Что означают слова "бегущая и неизменяющаяся волна"?
Только то, что если мы взглянем на профиль в определенный момент времени,
подождем, взглянем в другой момент времени, то мы увидим, что
профиль не изменится по всоему виду, а только немного сместится.
Уже исходя из этого наблюдения, можно записать главное уравнение,
описывающее волну:
f(x,t2) = f(x√v(t2-t1),t1)
Здесь v ≈ это некая константа, показывающая, насколько "шустро" смещается
профиль (она равна, разумеется, скорости волны).
Здесь я хочу особо остановиться на трех пунктах.
Первое: самое нетривиальное в этом уравнении, это то, что с обоих
сторон стоит одна и та же буквочка f. Это означает, что функция f
≈ не любая, а какая-то особенная: это самоподобная функция,
функция, которая равна самой себе, взятой при других агрументах.
Второе, перед нами ≈ не дифференциальное, не интегральное,
а функциональное уравнение. А функциональные уравнения -- самые сложные
уравнения в мире.
(Кто не верит, пусть попробует решить задачу: найти такую функцию
f(x), чтобы для всех x выполнялось f(f(x)) = exp(x). )
Третье, я хочу донести мысль, что выписанное здесь функциональное
уравнение является самым интуитивно понятным волновым уравнением,
самым непосредственным переводом слов "бегущая волна" на язык математики.
Это уравнение заключает в себе одну-единственную, но самую главную мысль:
волна ≈ это самоподобный профиль. И в физике нередко бывает так, что
всякие сложные дифуры на самом деле проистекают из одного прозрачного
функционального уравнения, которое схватывает самую суть.
Ну а теперь покажем, как получить из нашего функционального уравнения
всем известный волновой дифур.
Выписанное функциональное уравнение справедливо для любых значений
аргументов, в том числе и когда t2√t1 = dt ≈
дифференциально малому приращению. Но тогда
обе части уравнения f(x,t+dt) = f(x√v*dt,t) (где t1 заменили просто на t)
можно разложить в ряд Тейлора около точки x,t:
f(x,t) + дf(x,t)/дt * dt = f(x,t) √ v дf(x,t)/дx *dt
откуда получаем
дf(x,t)/дt + v дf(x,t)/дx = 0.
Казалось бы, все. И это пока не совсем похоже на общеизвестное волновое уравнение.
Дело в том, что мы пока получили волну немножко странного вида:
это волна, которая может распространяться только вправо.
Это не совсем то, что нам надо: мы хотим, чтобы у нас волны могли бежать
во всех направлениях. В нашей одномерной задаче это значит,
что функция волна f(x,t) должна мочь описывать волны, бегущие и влево.
То есть функция f(x,t) должна вдобавок удовлетворять уравнению
дf(x,t)/дt √ v дf(x,t)/дx = 0.
В итоге, уравнение, описывающее систему с волнами в обе стороны, есть
(д/дt √ v д/дx)(д/дt + v д/дx)f(x,t) = д2f(x,t)/дt2 √ v2 д2f(x,t)/дx2 = 0.
Напоследок, небольшое предостережение.
Проведенный вывод: это чисто кинематическое объяснение, почему
волновой дифур в самом деле описывает бегущую волну.
Это лишь некое размышление про свойства волн,
и ни в коем случае не может служить методом для выяснения,
существуют или нет волны
в той или иной системе. Для вывода же волн в конктерной системе надо пользоваться
честными и аккуратными динамическими уравнениями.
�


