Эффект Холла ≈ это явление, происходящее, когда проводник с током
помещают в магнитное поле. Движущиеся носители тока (например, электроны)
чувствуют присутствие магнитного поля и отклоняются им.
В результате, на боковых стенках проводника возникает разность потенциалов,
и она препятствует дальнейшему отклонению электронов (Рис.1).
| ═ |
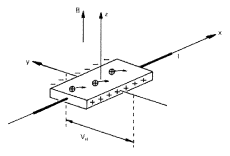
Рис.1 Классический эффект Холла в проводнике в магнитном поле.
═
|
Вроде все просто: есть ток, есть магнитное поле, чем больше поле, тем
большую лоренцеву силу надо компенсировать, и тем большая
возникает разность потенциалов. Простенький расчет показывает,
что разность потенциалов линейно зависит от величины магнитного поля.
Этот эффект ≈ классический, он не учитывает квантовых эффектов.
Квантовый эффект Холла, который возникает при очень сильных магнитных
полях, состоит в том, что зависимость холловской разности потенциалов
от магнитного поля вместо линейной становится ступенчатой, квантованной.
Для объяснения этого эффекта, в общем-то, особых усилий не требуется:
он хоть и требует знание квантовой механики, но может быть
объяснен и продвинутому школьнику.
Просто надо внимательно посмотреть на уравнение Шредингера для
частицы в магнитном поле и увидеть, что ступенька в этой зависимости
в самом деле наступает, когда электроны полностью заполняют целое число
уровней Ландау.
А вот дробный квантовый эффект Холла ≈ это когда
появляются ступеньки при дробном числе заполнения,
например, когда электроны заполняют одну треть нижнего уровня
Ландау ≈ оказался довольно крепким орешком
для теоретиков. Дело в том, что это уже эффект не просто квантовомеханический,
а эффект, могущий возникнуть только в конденсированной среде, что
сразу же усложняет задачу.
Обычно считается, что теоретическая конструкция Роберта Лаффлина
(за которую он в 1998 году, вместе с Хорстом Штормером и Даниелом Тсуи,
получил Нобелевскую Премию) столь сложна, что неподготовленному
читателю ее лучше и не рассказывать. Однако мне кажется есть
один момент, который можно объяснить на школьном примере.
Вот смотрите. В чем состоит основная трудность при описании любого
конденсированного вещества? В том, что решение уравнений, описывающих
движение каждой из частиц, а значит, формулу, описывающую
поведение всего вещества, просто так в лоб не получишь.
В чем состояла догадка Лаффлина? В том, что он сразу угадал
решение, ничего не решая. Он сразу взял и написал явный вид
волновой функции, описывающий сразу всю электронную жидкость
в магнитном поле. Ну а дальше все пошло-поехало, и через
десяток формул загадочное доселе явление было описано.
Мистика ли это? Оказывается, не совсем.
Оказывается, что если электроны "плавают" в сильном внешнем магнитном
поле, то им практически все равно, какие еще силы на них действуют.
"Практически все равно" означает, что есть ли между электронами притяжение
или отталкивание или же вообще нет никакого взаимодействия,
волновая функция всей жидкости от этого не меняется.
От этого меняется, конечно, ее энергия жидкости, но не сама
"форма" жидкости!
Как такое можно понять?
| ═ |
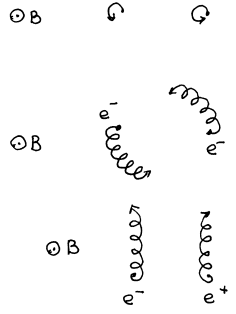
Рис.2 Заряженные частицы в сильном магнитном поле: нет взаимодействия между частицами
(верхний рисунок), отталкивание (средний рисунок), притяжение (нижний рисунок).
═
|
А давайте рассмотрим два электрона, находящихся в сильном магнитном
поле. Как мы знаем, если пренебречь взаимодействием электронов
друг на друга, то каждый их них под действием силы Лоренца вращался
бы по окружности, Рис.2, вверху. "Сильное" магнитное поле в нашем примере означает то,
что радиус орбиты во много раз меньше, чем расстояние между
электронами.
Включим теперь силы электростатического отталкивания. Думаете,
электроны разлетятся в разные стороны? Ничего подобного,
магнитное поле этого не допустит! Вместо этого ≈ как нетрудно
убедиться и старшекласснику ≈ электроны начнут медленно
дрейфовать друг вокруг друга, Рис.2, средний рисунок
(все-таки, скрещенное поле).
Дрейфовать ≈ по окружности!
Ну а если бы у нас был электрон и позитрон, то есть, притягивающиеся
частицы? Они бы тоже никуда не полетели, а начали бы дрейфовать,
но только параллельно друг другу, Рис.3, внизу.
Заметьте, что во всех трех случаях две частицы
образуют связанное состояние! Характер движения этого связанного
состояния несколько разный, но само наличие связанного состояния
≈ явление универсальное, не зависящее ни от силы, ни от знака,
ни вообще от наличия взаимодействия!
И теперь немножко понятно становится, "по какому праву" Лаффлин
написал волновую функцию электронного газа, ничего не решая.
Он просто нашел ту сердцевину явления, которая не зависит
от деталей взаимодействия. И эта находка и принесла
ему Нобелевскую премию.
Дотошный читатель спросит: а может, автор сумеет объяснить
и возникновение дробно-заряженных квазичастиц в двумерной
электронной жидкости в сильном магнитном поле?
Так же, на пальцах, через какую-нибудь простенькую задачку-аналогию.
Увы, пока не получилось. Может, кто поможет?
�



